Log Table Use Logarithm Table 2024– In mathematics, the logarithm table is used to find the value of a logarithmic function. The simplest way to find the value of a given logarithmic function is by using the log table. Here, the definition of the logarithmic function and the procedure for using the logarithm table are given in detail. Also, get the antilogarithm table here for reference. This means that the logarithm of a number is the exponent to which another fixed value, the base, must be raised to produce that number.
Log Table How to Use Logarithm Table
In other words, the logarithm of a number is the number of times the base number is multiplied by itself to produce that number. In simple cases, the logarithm counts the repeated multiplication. To find the value of a logarithmic function, you must use the log table. The logarithm table is highly effective in finding the value of a logarithmic function. One of the simple ways to determine the value of a given logarithmic function is with the help of log tables. Many students have difficulty using logarithm tables and antilog tables.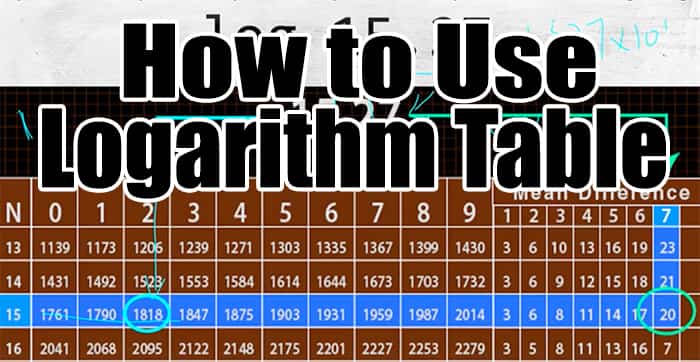
We have provided a log table pdf along with table definition on this page. Furthermore, we have explained in detail with examples how to use the logarithm table and the process of using antilogarithm table. Read on to know all about log tables. Before we provide you with the logarithm table from where you will get all the values, let us understand the concept of a logarithmic function. Logarithmic functions are the inverse of exponential functions.
Also Check Top 10 Longest River In India
Log Table: Concept & Definition
The logarithmic function is defined as the inverse function of the exponent. The logarithmic function is described as
For x, a > 0, and a≠1,
y = logarithm x, if x = ay
Then the logarithmic function is written as:
f(x) = log x
The most common bases used in logarithmic functions are base E and base 10. The log function with base 10 is called the general logarithmic function and is represented by log 10 or simply log.
f(x) = log 10
The log function for base e is called the natural logarithmic function and is represented by log.
f(x) = log x
Common logarithm [f(x) = log10x]: The logarithm of base 10 (ie b = 10) is called the general logarithm and has many applications in science and engineering.
Natural logarithm [f(x) = logex]: The base number of the natural logarithm is e (≈ 2.718). Due to its simple etymology, its use is widespread in mathematics and physics.
Binary logarithm [f(x) = log2x]: Binary logarithm uses base 2 (ie b = 2) and is commonly used in computer science.
Properties of Logarithms
Theorem 1: The logarithm of the product of two numbers, say a and b, is equal to the sum of the logarithms of the two numbers. Both numbers must have the same base. This theorem is also known as the “product rule for logarithms”.
Theorem 2: The division of two numbers is the antilog of the difference of the logarithms of the two numbers. In other words, the logarithm of the division of two numbers, such as a and b, is equal to the difference of the logarithm of the two numbers. Both numbers must have the same base. This theorem is also called the “quotient rule for logarithms”.
Theorem 3: The logarithm of a number from any other base can be determined by the logarithm of the same number for a given base.
Theorem 4: The logarithm of a number raised to a power is equal to the index of the power multiplied by the logarithm of the number. The basis of both is the same. This theorem is also known as the “power rule for logarithms”.
Common Logarithm Table for 1 To 10
| Common Logarithm to a Number (log10x) | Log Values |
| Log 1 | 0 |
| Log 2 | 0.3010 |
| Log 3 | 0.4771 |
| Log 4 | 0.6020 |
| Log 5 | 0.6989 |
| Log 6 | 0.7781 |
| Log 7 | 0.8450 |
| Log 8 | 0.9030 |
| Log 9 | 0.9542 |
| Log 10 | 1 |
Natural Logarithm Table for 1 to 10
| Natural Logarithm to a Number (logex) | Log Values |
| ln (1) | 0 |
| ln (2) | 0.693147 |
| ln (3) | 1.098612 |
| ln (4) | 1.386294 |
| ln (5) | 1.609438 |
| ln (6) | 1.791759 |
| ln (7) | 1.94591 |
| ln (8) | 2.079442 |
| ln (9) | 2.197225 |
| ln (10) | 2.302585 |
Steps to Use the Log Table
- Understand the concept of logarithms. Each log table is only usable with a fixed base. The most common type of logarithm table used is log base 10.
- Identify the characteristic part and mantissa part of the given number. For example, if you want to find the value of log10 (15.27), first separate the characteristic part and the mantissa part.
- attribute part = 15
- mantissa part = 27
- Use a common log table. Now, use row number 15 to check column number 2, and write the corresponding value. So the value obtained is 1818.
- Use the logarithm table with the mean difference. Slide your finger in the mean difference column number 7 and row number 15, and write the corresponding value as 20.
Add up both the values obtained in Step 3 and Step 4. This is 1818+20 = 1838. Therefore, the value 1838 is the mantissa portion. - Find the attribute part. Since the number is between 10 and 100, (101 and 102), the attribute part must be 1.
- Finally, add both the characteristic part and the mantissa part, this becomes 1.1838.
FAQs to Use Log Table
How do you calculate logarithms?
To calculate logarithms, you need to know the base 10 logarithm and the exponent. The base 10 logarithm is simply a number that tells you how many times a number has been multiplied by 10. So, for example, 2 (base 10 logarithm) would be written as 2 x 10 or 20. The exponent is simply a number that tells you how many times the base 10 logarithm needs to be raised to get to the decimal place. So, for example, if we wanted to calculate the logarithm of 101 (base 10), we would use the following equation: log(101) = 3. 14159 The logarithm of 100 (base 10) would be written as 2.10 and the logarithm of 1010 (base 10) would be written as 3.14159265359.
How do you use log tables for multiplication and division?
To use log tables for multiplication and division, you need to understand the following concepts: 1. Logarithms are a mathematical function that relate a base number (10, 100, 1000) to a power (2, 3, 10). 2. The table below shows how to multiply two numbers using the logarithm function. 3. To divide two numbers using the logarithm function, you need to find their corresponding entries in the table and use the correct line on the graph. 4. To find the inverse of a number using the logarithm function, you first need to find its exponent and then use that information to find its corresponding entry in the table.
How do you solve logs using a table?
In order to solve logs using a table, you need to first identify the columns in the table that contain the data you want to analyze. Next, you need to create a query that will return the data in those columns. Finally, you can use the results of that query to plot or graph your data.
Check Also

